Different types of polymorphism in C++ and Java

 

GREEDY ALGORITHM AND IT’S USE

INTRODUCTION

Imagine you are going for hiking and your goal is to reach the highest peak possible. You already have the map before you start, but there are thousands of possible paths shown on the map. You are too lazy and simply don’t have the time to evaluate each of them. Screw the map! You started hiking with a simple strategy – be greedy and short-sighted. Just take paths that slope upwards the most. This seems like a good strategy for hiking. But is it always the best?

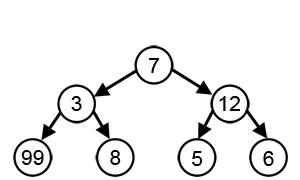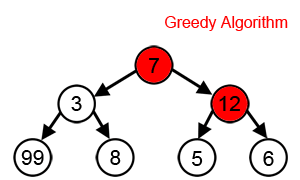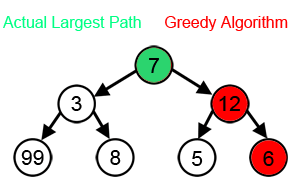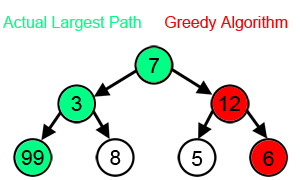
After the trip ended and your whole body is sore and tired, you look at the hiking map for the first time. Oh my god! There’s a muddy river that I should’ve crossed, instead of keep walking upwards. This means that a greedy algorithm picks the best immediate choice and never reconsiders its choices. In terms of optimizing a solution, this simply means that the greedy solution will try and find local optimum solutions - which can be many - and might miss out on a global optimum solution.

FORMAL DEFINATION

“Greedy algorithms aim to make the optimal choice at that given moment. Each step it chooses the optimal choice, without knowing the future. It attempts to find the globally optimal way to solve the entire problem using this method.”

 

WHY ARE GREEDY ALGORITHMS CALLED GREEDY?

 We call algorithms greedy when they utilize the greedy property. The greedy property is:

 At that exact moment in time, what is the optimal choice to make?

 Greedy algorithms are greedy. They do not look into the future to decide the global  optimal solution. They are only concerned with the optimal solution locally. This  means that the overall optimal solution may differ from the solution the  algorithm chooses. They never look backwards at what they've done to see if they could optimize globally. This is the main difference between Greedy and Dynamic Programming.

To be extra clear, one of the most Googled questions about greedy algorithms is: "What problem-solving strategies don't guarantee solutions but make efficient use of time?" .The answer is "Greedy algorithms". They don't guarantee solutions, but are very time efficient.

PROPERTIES OF GREEDY ALGORITHM

 Greedy Algorithms can be applied to problems following two basic conditions:

      1. Greedy Choice Property: A global optimum can be reached by selecting  the local optimums.

 2.  Optimal Substructure Property: A problem follows optimal substructure  property if the optimal solution for the problem can be formed on the basis  of the optimal solution to its subproblems.

    Little Technical Part

Here you can see the greedy property.

      EXAMPLES/PROBLEMS ON GREEDY ALGORITHM

        

    Activity Selection Problem

     The problem statement for Activity Selection is that "Given a set of n activities   with their start and finish times, we need to select maximum number of non- conflicting activities that can be performed by a single person, given that the person can handle only one activity at a time." The Activity Selection problem follows Greedy approach i.e. at every step, we can make a choice that looks  best at the moment to get the optimal solution of the complete problem.

   Our objective is to complete maximum number of activities. So, choosing the  activity which is going to finish first will leave us maximum time to adjust the later activities. This is the intuition that greedily choosing the activity with earliest  finish time will give us an optimal solution. By induction on the number of choices made, making the greedy choice at every step produces an optimal solution, so we chose the activity which finishes first. If we sort elements based on their starting time, the activity with least starting time could take the maximum duration for completion, therefore we won't be able to maximize number of  activities.

Activity-Selection(Activity, start, finish)

     Sort Activity by finish times stored in finish

     Selected = {Activity[1]}

     n = Activity.length

     j = 1

     for i = 2 to n:

         if start[i] ≥ finish[j]:

             Selected = Selected U {Activity[i]}

             j = i

 return Selected

      Complexity

      Time Complexity:
      When activities are sorted by their finish time: O(N) When activities are not sorted by their finish time, the time complexity is O(N log N) due to complexity  of sorting.

Greedy approach vs Dynamic programming

 

A Greedy algorithm is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to a global solution are best fit for Greedy.

For example, consider the Fractional Knapsack Problem. The local optimal strategy is to choose the item that has maximum value vs weight ratio. This strategy also leads to global optimal solution because we allowed taking fractions of an item.

Dynamic programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial. For example, if we write a simple recursive solution for Fibonacci Numbers, we get exponential time complexity and if we optimize it by storing solutions of subproblems, time complexity reduces to linear.

 

             ADVANTAGES AND DISADVANTAGES

It is quite easy to come up with a greedy algorithm (or even multiple greedy algorithms) for a problem. Analyzing the run time for greedy algorithms will generally be much easier than for other techniques (like Divide and conquer). For the Divide and conquer technique, it is not clear whether the technique is fast or slow. This is because at each level of recursion the size of gets smaller and the number of sub-problems increases.

The difficult part is that for greedy algorithms you have to work much harder to understand correctness issues. Even with the correct algorithm, it is hard to prove why it is correct. Proving that a greedy algorithm is correct is more of an art than a science. It involves a lot of creativity. Usually, coming up with an algorithm might seem to be trivial, but proving that it is actually correct, is a whole different problem.

Regards,

Shrawani Shinde